NP problem
P, NP, NP-complete problem
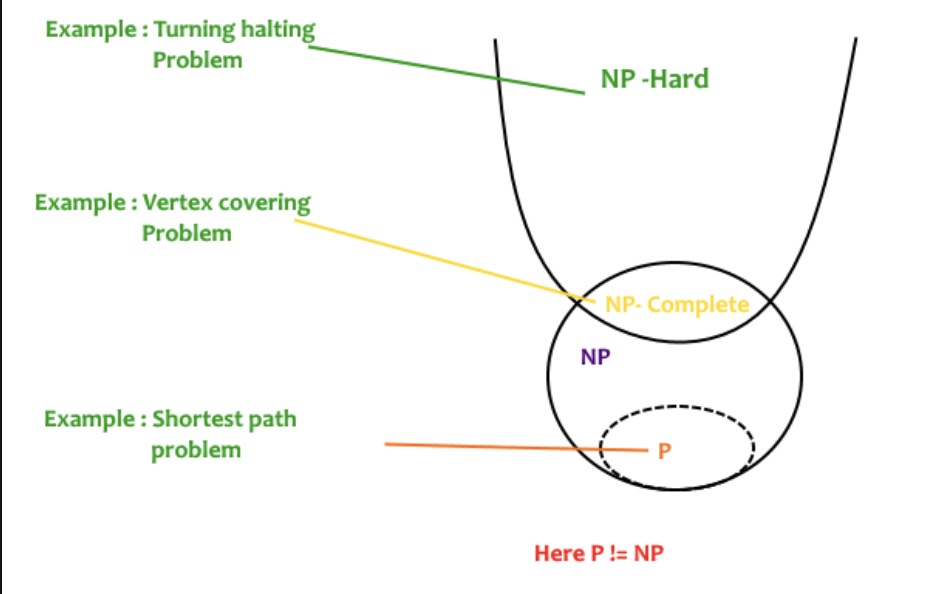
Figure 1: NP problem
P
A set of problems that can be solved by a deterministic Turing machine in polynomial-time.
NP
The NP problems is a set of decision problems that can be solved by a Non-deterministic Turing Machine in polynomial-time, P is a subset of NP(any problem that can be solved by a deterministic machine in polynomial time can also be solved by a non-deterministic machine in polynomial time)
Informally, NP is a set of decision problems that can be solved by a polynomial-time via a lucky algorithm, a magical algorithm that always makes a right guess among the given set of choices.
NP-complete
NP-complete problems are the hardest problems in the NP set. A decision problem L is NP-complete if:
- L is in NP(Any given solution for NP-complete problems can be verified quickly, but there is no efficient known solution)
- Every problem in NP is reducible to L in polynomial time
NP-Hard
A problem is NP-hard if it follows property 2 mentioned above, and doesn’t need to follow property 1. Therefore, the NP-complete set is also a subset of the NP-hard set.
Some question
Decision vs optimization
NP-completeness applies to the realm of decision problems. Because it’s easier to compare the difficulty of decision problems than that of optimization problems.