PID Controller
Contents
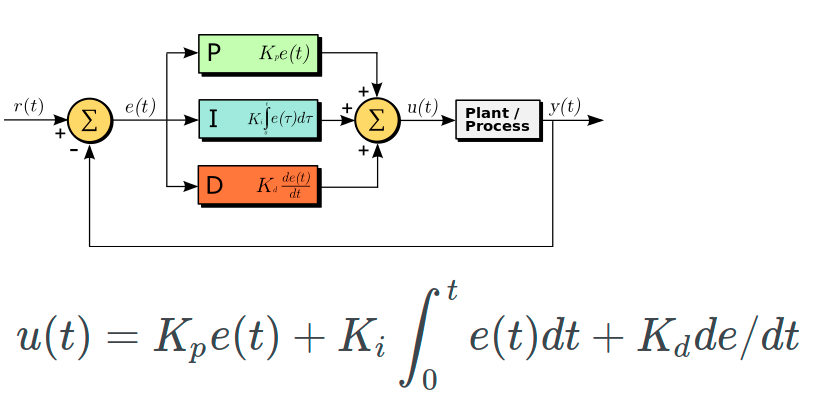
Proportional-integral-derivative controller is the classical control strategy. In this blog, I use python to write a primitive PID controller.
PID Control
import time
import matplotlib.pyplot as plt
from scipy.interpolate import make_interp_spline
import numpy as np
class PID:
def __init__(self, P=0.2, I=0.0, D=0.0, current_time=None):
self.Kp = P
self.Ki = I
self.Kd = D
self.current_time = current_time if current_time is not None else time.time()
self.last_time = self.current_time
self.ControlPoint = 0.0
self.last_error = 0.0
self.PTerm = 0.0
self.ITerm = 0.0
self.DTerm = 0.0
self.windup_guard = 20.0
def step(self, feedback_value, current_time=None):
error = self.ControlPoint - feedback_value
delta_error = error - self.last_error
self.current_time = current_time if current_time is not None else time.time()
delta_time = self.current_time - self.last_time
if (delta_time >= 0):
self.PTerm = self.Kp * error
self.ITerm += error * delta_time
if delta_time > 0:
self.DTerm = delta_error / delta_time
self.last_time = self.current_time
self.last_error = error
self.output = self.PTerm + (self.Ki * self.ITerm) + (self.Kd * self.DTerm)
t0 = 9
t_end = 50
pid = PID(1.2, 1.0, 0.001)
feedback = 0
feedback_list = []
time_list = []
controlpoint_list = []
for t in range(1, t_end):
pid.step(feedback)
output = pid.output
if pid.ControlPoint > 0:
feedback += output
if t > t0:
pid.ControlPoint = 1/t
time.sleep(0.02)
feedback_list.append(feedback)
controlpoint_list.append(pid.ControlPoint)
time_list.append(t)
time_index = np.array(time_list)
time_smooth = np.linspace(time_index.min(), time_index.max(), 300)
spline = make_interp_spline(time_list, feedback_list)
feedback_smooth = spline(time_smooth)
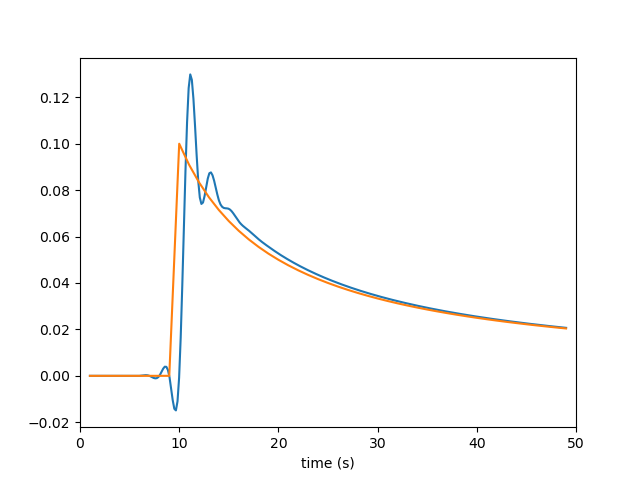
plt.plot(time_smooth, feedback_smooth)
plt.plot(time_list, controlpoint_list)
plt.xlim((0, t_end))
plt.xlabel('time (s)')
plt.savefig('/Users/jiawei/Documents/roam/note/images/pid.png')